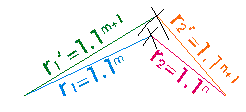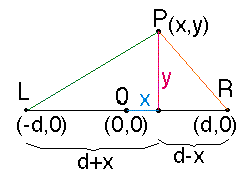If the families of circles were arithmetically spaced,
the moiré  patterns would be hyperbolas,
that is points p such  D(f1, p) - D(f2, p) = k  (k a constant) Hyperbola moiré pics.

I had asked in sci.math if the Moirés are circles in these exponentially spaced  circles.

Chas Brown replied with this explanation:

D(f1,p)/D(f2,p) = k, k constant.

Consider some point of intersection of two circles, with radii r1 and r2, respectively. Then exists some m and n such that 
r1 = (1.1)^m and
r2 = (1.1)^n

The "next intersection" in the Moire pattern will be at 
r1' = (1.1)^(m+1) = 1.1*r1 and
r2' = (1.1)^(n+1) = 1.1*r2

thus r1'/r2' = r1/r2

If you take your Moire pattern "to the limit", you're looking at two circle families, centered say at (-d, 0) and (d,0). Let the family of circles have radii u^n, n an integer, and u>1.0. As u gets very close to 1, the sucessessive steps in the pattern get smaller, but we still get the same pattern noted above (imagine u = (1.1)^(1/1000)); same pattern, with 1000 intervening steps). As u approaches 1, the Moire paten becomes the family curves, each of which is the locus of points with radii to the respective generating circles in a fixed ratio, say c.
Thus it is the locus of points P in the triangle below with LP/PR=c. (L being the center of the left circle, R being the center of the right circle).

A little trigonometry (Pa the perpendicular through P has length y, OA length x) shows that these points P satisfy, for some constant C:
(y^2 + (x+d)^2) / (y^2 + (d-x)^2) = c^2

where c is the fixed ratio of LP/PR (here I'm assuming c>1), and d is the distance of the generating circles from the origin. We can then expand this to:
(c^2-1)*y^2 + (c^2-1)*x^2 - 2*(c^2+1)*d*x + (c^2-1)*d^2 = 0

since c is a constant, let k = (c&2+1)/(c^2-1); k > 1 since 1 < c < infinity, then

y^2 + x^2 - 2*k*d*x + d^2 = 0
y^2 + x^2 - 2*k*d*x = k^2*d^2 + d^2 = 0
y^2 + (x - k*d)^2 - (k^2-1)*d^2 = 0

so

y^2 + (x - k*d)^2 = (k^2-1)*d^2

is the equation of the family of circles you see, with 1 < k < infinity.

The same follows if we choose c < 1; in that case k has range
-infinity < k < -1, and the circles are on the other side of the y-axis. c=0 gives us the line x=0