 |
|
- This is Escher's rendering of a stellated dodecahedron, the polyhedron which the next fractal is based on. |
Again, I do something similar but in three dimensions. Below is Kepler's
stellated dodecahedron.
Smaller stellated dodecahedra can be placed within the stellated dodecahedron's
pyramids.
-
An article on Keplerian solids appears in "Computers and Graphics"
Vol. 19, No. 6, pp. 885-888, 1995
-
-
 |
|
- This Escher drawing is a wonderful depiction of two interpenetrating tetrahedra, aka a stellated octahedron, the polyhedron which the next fractal is based on. |
-
-
Kepler was able to stellate the octahedron by extending its faces.
The stellated octahedron is also two interpenetrating tetrahedra,
kind of a three dimensional version of the Star of David
-
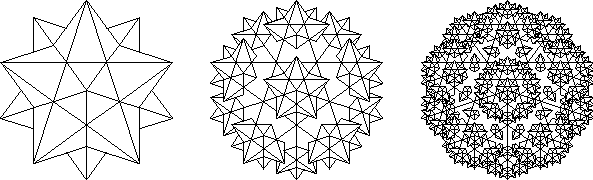
Just as with the Koch flake, place a smaller version of this solid
within each pyramid.
-
I was amazed when this critter started approaching the shape of a cube.
-
-
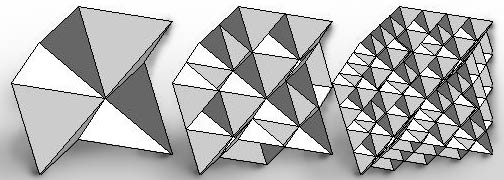
Imagine this cube as an ice cube. There are bubbles beneath the cube's
surface.
This the floor of the cube for the first three iterations.
In the first iteration there are two triangles for each of the cubes
bottom four edges.
These triangles form one fourth of an octahedron's surface.
-
As this fourth of an octahedron is divided by penetrating tetrahedra,
smaller half octahedrons and quarter octahedrons result.
-
Then divided again by penetrating tetrehedrons, smaller full octahedral
bubbles are isolated beneath the cube's surface.
-
With each iteration these bubbles grow more complex, forming a fractal
in their own right.
-
-
The first few iterations of the octahedral bubble fractal viewed from
three different angles.
-